Maya getallen en telstelsels

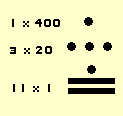
De Maya’s gebruikte een teleenheid vantwintig. alle getallen werden van 0 tot en met 20 geschreven en daarna 1 maal 20plus daaronder het resterende getal. In de derde lijn komen de aantal keren dat400 voorkomt in een getal en eventueel daar weer boven 8000-tallen. Rechts is een voorbeeld van 471.
Naast het getal twintig waren er nog anderegetallen belangrijk voor de Maya’s. Zo werd het getal 9 vereerd en is in veleberekeningen het sleutelgetal. Ook 260 (13 x 20) is een heel belangrijkgetal. Het is het getal van de ‘Tjolkin’ de ‘heilige’ korte kalender. Dit getalkomt tot stand door de vermenigvuldiging van de rotatietijden van de zon op deevenaar en de polen (26 dagen om 37 dagen). Dit is pas door recentelijk ruimteonderzoek duidelijk geworden voor ons. Het getal werd door de Maya’sgebruikt om voorspellingen te doen en astronomische gebeurtenissen te volgen.
Daarnaast hadden de Maya’s ook nog een langekalender van 18 ‘maanden’ van 20 dagen en vijf naamloze dagen (365 dagen).
Deze twee kalenders werden naast elkaargebruikt en na 18.980 dagen (52 jaar) komen de kalenders weer tegelijk bij hun1e dag.
De Maya’s gebruikte de cycli van 144.00dagen, 7.200 dagen, 360 dagen en 20 dagen om de tijd te meten, die werd berekendvanaf de geboorte van Venus in het jaar 3113 v. Chr.. De manier om tijd te uit te drukken gebeurdein de volgende eenheden:
| Baktun | Katun | Tun | Uinal | Kin |
| 144.000 | 7.200 | 360 | 20 | 1 |
| Dagen | Dagen | Dagen | Dagen | Dag |
Ook deze eenheden zijn niet zomaar gekozen want als men de volgenderekensom bekijkt komt er voor de Maya’s weer een belangrijk getaluit: 144.000+7.200+360+20 x 9= 1.366.560.
Dit is zogenoemd het zonnevlekgetal,de catastrofeperiode, het getal dat voor de Maya’s de geboorte van Venus aangaftot de dag van catastrofale vernietiging van de aarde.
Naast dit grote getal hadden de Maya’s een nog grotere cyclus: 13 Baktun,oftewel 1.872.000 dagen.Deze grote cyclus begint op 13 augustus 3114 v.Chr. in de gregoriaanse kalender en eindigt op 22 december 2012.
De Maya’s wisten dat wat betreft hetzonnejaar van de 365 dagen van de kalender kon worden verbeterd. De schattingvan de maya’s was gebaseerd op 365,2420 dagen, terwijl de moderne astronomie dieperiode op 365,2422 heeft vastgesteld. De afwijking is dus dan 17 seconden opeen heel jaar.
Met betrekking tot de maancirkel heeft mentwee berekeningen: de eerste heeft 405 maanlopen, oftewel 46 heilige jaren van260 dagen, dus 11960 dagen. De moderne astronomie heeft deze duur vastgesteld op11959.888 dagen. De afwijking is dan 32 seconden op 190 maanlopen (ruim 135jaar). De tweede berekening heeft 4400 dagen op 149 maanlopen, waar de moderneastronomie 4400,0574 dagen telt, wat neerkomt op 29.530587 dagen per maanloop,terwijl de benadering van de Maya’s overeenkomt met 29.53020 dagen. Dezeberekening van astrologen uit Copán in 682 wijkt dus maar 33 seconden en 43/100per maanloop af.
Het Venusjaar van de Maya’s was geschat op584 dagen, terwijl de moderne wetenschap dit heeft berekend op 583,92 dagen.Maar de planeet Venus draait in 224 dagen en 7 uur om de zon – iets wat demaya’s niet wisten. Zij gingen ervan uit dat de Aarde centraal was en daar allesomheen draaide.
Hoe hebben de maya’s, die noch overinstrumenten beschikten die uren, minuten of seconden konden meten, noch overoptische apparaten of hoekmeters, tot zulke verbluffende resultaten kunnenkomen? De oplossing ligt in de eeuwenlange observaties gecombineerd metrekenkundige gegevens.
